Лабораторная работа № 4: «Изучение гидравлических сопротивлений напорного трубопровода»

Автор: Евгений Коноплев

к.т.н., профессор

Автор: Илья Образцов

к.т.н., ведущий инженер ИРТ ТвГТУ

Автор: Александр Яблонев

д.т.н., зав. кафедрой ГТиГП

Лабораторная работа № 4: «Изучение гидравлических сопротивлений напорного трубопровода с определением коэффициентов гидравлического трения и местных сопротивлений».

Вводная часть

Экспериментальными исследованиями установлено, что при движении жидкости часть полного напора (энергии) затрачивается на преодоление работы сил вязкости и инерции, т.е. возникают потери напора.

При равномерном движении жидкости гидравлическое сопротивление, проявляющееся равномерно по всей длине потока, называют сопротивлением по длине, а вызываемые им потери напора ‒ потерями напора по длине \((h_l)\). Эти потери в круглых трубопроводах, работающих полным сечением, вычисляют по формуле Дарси-Вейсбаха:

\(h_l = \lambda \frac{l}{d} \frac{v^2}{2g} \), (11)

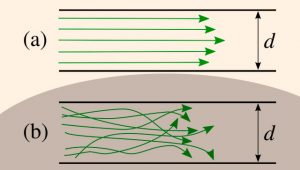
где \(\lambda\) ‒ безразмерный коэффициент, называемый коэффициентом гидравлического трения (коэффициентом Дарси). Величина коэффициента \(\lambda\) характеризует гидравлическое сопротивление трубопровода и зависит в общем случае от числа Рейнольдса \(Re\) и относительной шероховатости \(\Delta_э/d\) трубопровода, т.е. \(\lambda = f(Re, \Delta_э/d)\); \(l\) и \(d\) – длина и внутренний диаметр трубопровода; \(v\) – средняя скорость движения потока жидкости.

Величину коэффициента \(\lambda\) при гидравлических экспериментах вычисляют по опытным данным из формулы (11). При гидравлических же расчетах – по эмпирическим и полуэмпирическим формулам, например, при ламинарном режиме:

\(\lambda = \frac{64}{Re} \), (12)

а при турбулентном режиме движения жидкости и работе трубопровода в области доквадратичного сопротивления – по формуле А.Д. Альтшуля:

\(\lambda_{докв} = 0,11 (\frac{\Delta_э}{d} + \frac{68}{Re})^{0,25} \), (13)

Величину абсолютной эквивалентной шероховатости \(\Delta_э\) при расчетах берут из справочной литературы в зависимости от материала трубопровода и состояния его внутренней поверхности. Например, для труб из органического стекла \(\Delta_э = 0,006\ мм\), а для стальных водопроводных умеренно заржавленных труб \(\Delta_э = 0,20…0,50\ мм\).

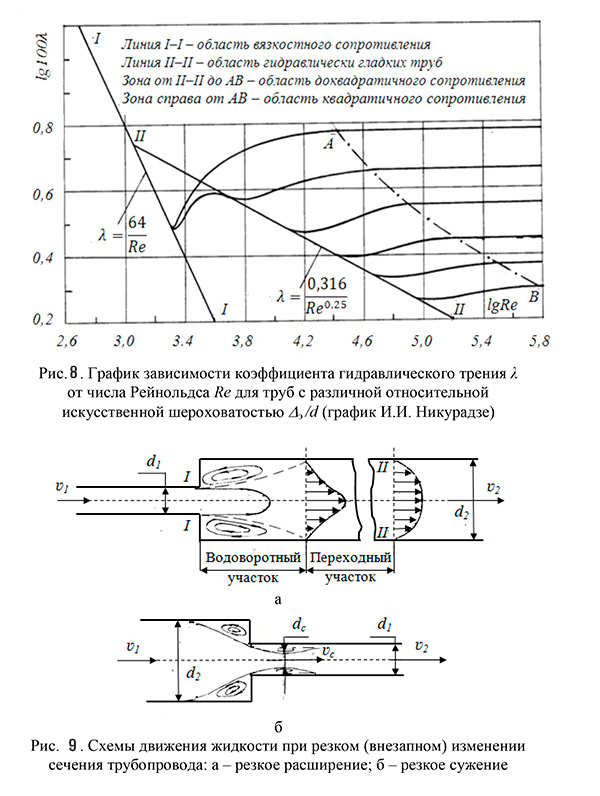
Область гидравлического сопротивления при расчетах определяют или непосредственно по графикам \(\lambda = f(Re, \Delta_э/d)\), полученным опытным путем для труб из различных материалов и приведенным в справочной литературе, например, по графику Никурадзе (рис. 8), или с помощью соотношений \(\frac{10d}{\Delta_э}\) и \(\frac{500d}{\Delta_э}\), предложенных А.Д. Альтшулем на основе использования упомянутых графиков. В последнем случае вычисляют соотношения \(\frac{10d}{\Delta_э}\) и \(\frac{500d}{\Delta_э}\) и сравнивают их с числом Рейнольдса \(Re_{(d)} = \frac{vd}{\nu}\).

При этом, если \(Re \ge \frac{500d}{\Delta_э}\), трубопровод работает в области квадратичного сопротивления. Если \(Re \le \frac{10d}{\Delta_э}\), трубопровод работает в области гидравлически гладких труб. Если же \(\frac{10d}{\Delta_э} \lt Re \lt \frac{500d}{\Delta_э}\), трубопровод работает в области доквадратичного сопротивления.

Следует иметь в виду, что для каждой области гидравлического сопротивления предложены и используются при гидравлических расчетах свои формулы для вычисления коэффициента \(\lambda\).

Другой вид гидравлических сопротивлений, возникающих в местах резкого изменения конфигурации потока – изменение скорости потока по величине или направлению, называют местными сопротивлениями, а вызываемые ими потери напора ‒ местными потерями напора \((h_м)\).

При прохождении через любое местное сопротивление поток жидкости деформируется (рис. 9), вследствие чего движение становится неравномерным, резко изменяющимся, для которого характерны:

а) значительное искривление линий тока и живых сечений потока;
б) отрывы транзитной струи от стенок трубопровода (ввиду действия закона инерции) и возникновение в местах отрыва устойчивых водоворотов;
в) повышенная (по сравнению с равномерным движением) пульсация скоростей и давлений;
г) изменение формы (переформирование) эпюр скоростей.

Местные потери напора при гидравлических расчетах вычисляют по формуле Вейсбаха :

\(h_м = \zeta \frac{v^2}{2g} \), (14)

где \(\zeta\) ‒ безразмерный коэффициент, называемый коэффициентом местного сопротивления; \(v\) ‒ средняя скорость потока в сечении за местным сопротивлением, т.е. ниже по течению (если скорость \(v\), как исключение, принимается перед местным сопротивлением, это обязательно оговаривается).

Величина коэффициента \(\zeta\) зависит в общем случае от числа Рейнольдса \(Re\), от вида и конфигурации, т.е., формы проточной части местного сопротивления. В частном случае, когда трубопровод, на котором расположено местное сопротивление, работает в области квадратичного сопротивления, величина коэффициента \(\zeta\) от \(Re\) не зависит.

Величину \(\zeta\) для каждого вида местного сопротивления определяют по данным гидравлических экспериментов, пользуясь формулой (14). Полученные таким образом значения коэффициентов \(\zeta\) для различных видов местных сопротивлений берутся при гидравлических расчётах (обычно при квадратичной области сопротивления) из справочной и специальной литературы. Исключением являются резкое расширение и резкое сужение трубопровода, для которых численные значения коэффициентов \(\zeta\) определяются по формулам, полученным теоретическим и полуэмпирическим путем. При резком расширении трубопровода, когда средняя скорость в формуле (14) взята перед местным сопротивлением, т.е. \(v_1\), коэффициент местного сопротивления от резкого расширения \(\zeta_{pp}^{′}\) равен:

\(\zeta_{pp}^{′} = (1 — \frac{S_1}{S_2})^2 \), (15)

где \(S_1\) и \(S_2\) ‒ площади проходных сечений трубопровода, соответственно, до и после местного сопротивления по направлению движения жидкости.

Если же скорость берется за местным сопротивлением, т.е. \(v_2\), то

\(\zeta_{pp}^{″} = (\frac{S_2}{S_1} — 1)^2 \), (16)

Коэффициент местного сопротивления при резком сужении трубопровода \(\zeta_{pc}\) принято относить к скорости после сужения. При этом

\(\zeta_{pc} = 0,5 (1 — \frac{S_1}{S_2})^2 \), (17)

Описание установки

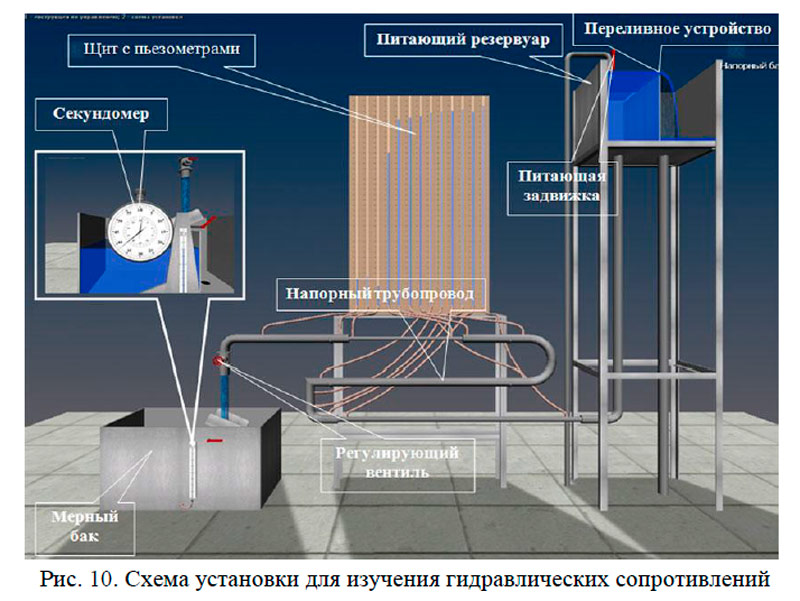
Установка (рис. 10) представляет собой напорный трубопровод с последовательно расположенными на нем гидравлическими сопротивлениями (по длине и местными). К каждому гидравлическому сопротивлению подключено по два пьезометра (перед и за ним). Все пьезометры для удобства работы выведены на щит. Для регулирования расхода воды \(Q\) в системе служит вентиль. Величина \(Q\) измеряется с помощью мерного бака и секундомера. Подача воды в систему осуществляется из питающего резервуара по трубе открытием задвижки. Постоянный уровень воды в питающем резервуаре (для обеспечения установившегося движения в системе) поддерживается переливным устройством.

Кинематический коэффициент вязкости воды в данной работе принимается по справочнику в зависимости от ее температуры, задаваемой преподавателем. Величина абсолютной эквивалентной шероховатости труб \(\Delta_э\) также задается преподавателем.

Схема установки для изучения гидравлических сопротивлений

Цель работы:

Определить по опытным данным, воспользовавшись формулами (11) и (14), значения коэффициента гидравлического трения \(\lambda_{оп}\) и величины коэффициента \(\zeta_{оп}\) для трех видов местных сопротивлений;
Установить, воспользовавшись соотношениями А.Д. Альтшуля области гидравлического сопротивления, в которых работали участки напорного трубопровода;
Вычислить значения коэффициентов гидравлического трения \(\lambda\) по соответствующим эмпирическим формулам;
Найти справочные значения коэффициентов местных сопротивлений;
Оценить сходимость \(\lambda_{оп}\) и \(\zeta_{оп}\) с их расчетными (справочными) значениями.
Построить по опытным данным (в масштабе) график напоров для участка, предложенного преподавателем.

Порядок выполнения работы и обработка опытных данных

Открыть питающую задвижку и наполнить установку водой.
После наполнения водой резервуара и стабилизации уровня воды в нем (переливное устройство должно при этом работать), следует открытием регулирующего вентиля подать воду в систему трубопроводов.
По секундомеру определить время \(t\ (с)\) наполнения мерного бака объемом \(W = 0,05\ м^3\).
Определить расход воды: \(Q = W/t\ (м^3/с)\).
Измерить: отметки уровней воды в пьезометрах для участков, указанных преподавателем, а также ее температуру (термометром в питающем резервуаре).
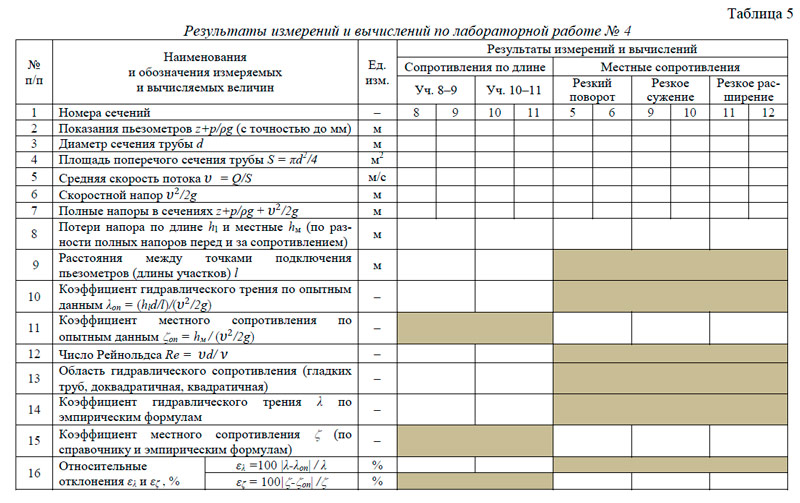
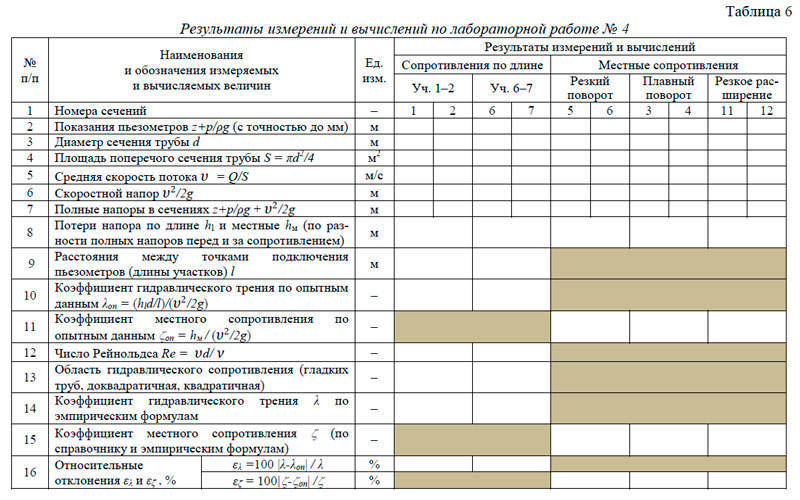
Результаты измерений для одного опыта (при одном расходе воды) записать в табл. 5–7 (в зависимости от участков, указанных преподавателем).
Произвести обработку опытных данных в табл. 5–7.
Построить по опытным данным (в масштабе) график напоров для участка, предложенного преподавателем.
Сформулировать заключение и выводы по результатам работы.

Основные контрольные вопросы к лабораторной работе № 4

Напишите и поясните формулы Дарси-Вейсбаха и Вейсбаха.
Как опытным путем определяют величины коэффициентов \(\lambda\) и \(\zeta\)?
Что характеризуют коэффициенты \(\lambda\) и \(\zeta\), от каких факторов в общем случае они зависят и как их определяют при гидравлических расчетах?
Объясните, что такое \(\Delta_э\) и \(\Delta_э/d\), как найти величину \(\Delta_э\) при гидравлических расчетах?
Назовите области гидравлического сопротивления трубопроводов и объясните, как определяют область сопротивления при гидравлических расчетах.
Изобразите схемы движения жидкости при резком повороте трубы на 90°, а также при резком расширении и резком сужении трубопровода и дайте пояснения к ним, указав, что характерно для движения потока при протекании его через любое местное сопротивление.
Изобразите схему графика Никурадзе и дайте пояснения.
Поясните понятия «гидравлически гладкая труба» и «шероховатая труба».
Назовите факторы, обуславливающие повышение потери напора при прохождении потока жидкости через местные сопротивления.
Докажите, воспользовавшись формулами Дарси-Вейсбаха и Блазиуса, что при работе трубопроводов в области гидравлически гладких труб \(h_l = f(v^{1,75} )\).