Лабораторная работа № 3: «Экспериментальная иллюстрация ламинарного и турбулентного режимов движения жидкости»

Автор: Евгений Коноплев

к.т.н., профессор

Автор: Илья Образцов

к.т.н., ведущий инженер ИРТ ТвГТУ

Автор: Александр Яблонев

д.т.н., зав. кафедрой ГТиГП

Лабораторная работа №3: «Экспериментальная иллюстрация ламинарного и турбулентного режимов движения жидкости, установление законов гидравлического сопротивления и определение критического числа Рейнольдса».

Вводная часть

Многочисленными экспериментальными исследованиями установлено, что движение жидкости может происходить или при ламинарном, или при турбулентном режиме.

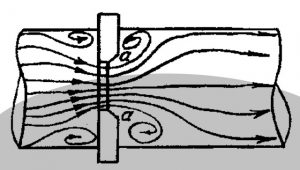
Ламинарный режим наблюдается при небольших скоростях движения. При этом окрашенные струйки жидкости не перемешиваются, сохраняясь по всей длине потока, т.е. движение жидкости при ламинарном режиме является струйчатым, перемешивание частиц жидкости отсутствует. Турбулентный режим наблюдается при значительных скоростях и характеризуется интенсивным перемешиванием частиц жидкости, что обуславливает пульсацию скоростей и давления.

Средняя скорость потока, при которой происходит смена режима движения жидкости, называется критической \((v_{кр})\). Величина ее, как показывают опыты в трубопроводах круглого сечения, зависит от рода жидкости, характеризуемого динамическим коэффициентом вязкости \(\mu\) и плотностью \(\rho\), а также от диаметра трубопровода \(d\). Одновременно опытами установлено, что величина безразмерного алгебраического комплекса, отвечающего критической скорости \(v_{кр}\):

\(Re_{кр(d)} = \frac{v_{кр}\rho d}{\mu} = \frac{v_{кр} d}{\nu} \approx 2320 = const \), (9)

\(Re_{кр(d)} = 2320\), называется критическим числом Рейнольдса.

Устойчивый ламинарный режим движения жидкости наблюдается при значениях числа Рейнольдса \(Re_{(d)} = \frac{v d}{\nu} \lt Re_{кр(d)} \approx 2320\), а турбулентный – при \(Re_{(d)} = \frac{v d}{\nu} \gt Re_{кр(d)} \approx 2320\).

Таким образом, число Рейнольдса:

\(Re_{(d)} = \frac{v d}{\nu} \), (10)

является критерием, позволяющим судить о режиме движения жидкости в круглой трубе, работающей полным сечением.

Величину \(\nu = \frac{\mu}{\rho}\), имеющую размерность \([м^2/с]\), входящую в формулы (9) и (10), называют кинематическим коэффициентом вязкости жидкости.

Из изложенного следует, что для определения режима напорного движения жидкости в круглом трубопроводе достаточно вычислить по формуле (10) число Рейнольдса, и сравнить его с критическим.

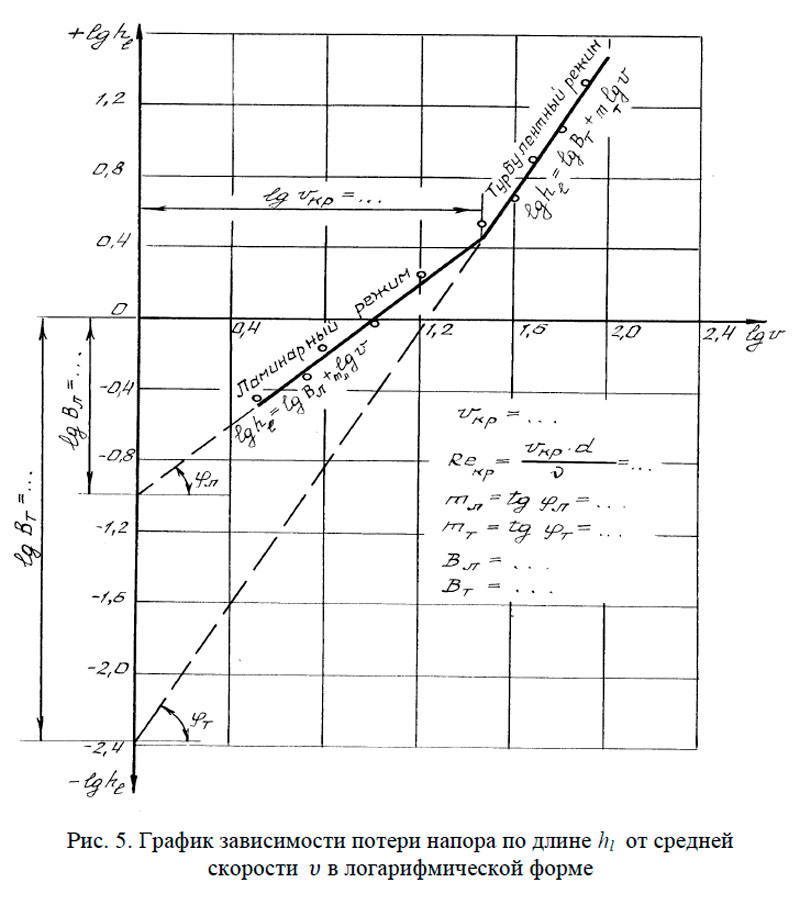
Знание режима движения жидкости необходимо для правильной оценки потерь напора при гидравлических расчетах. Как показывают опыты в круглых трубах при напорном равномерном движении (результаты их представлены на рис. 5 в виде графика зависимости потерь напора по длине \(h_l\) от средней скорости \(v\)), при ламинарном режиме потери напора \(h_l\) пропорциональны средней скорости \(v\) в первой степени, а при турбулентном ‒ в степени \(1,75 ≤ m ≤ 2\). Заметим, что с помощью этого графика определяют величину критической скорости \(v_{кр}\), а через нее ‒ и критическое число Рейнольдса по формуле (9).

потери напора по длине от средней скорости в логарифмической форме

Описание установки

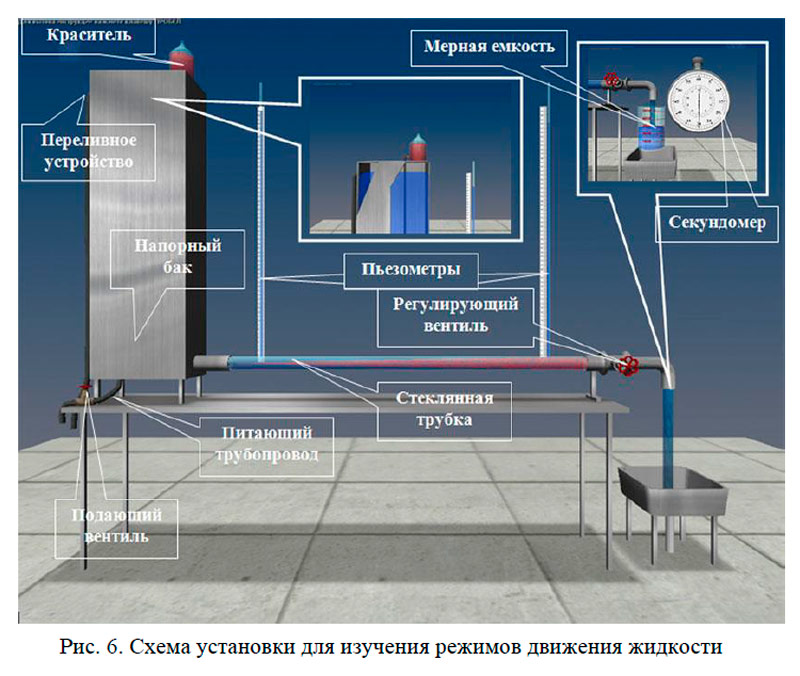
Установка (рис. 6) включает в себя расположенную горизонтально стеклянную трубу, в которой и изучается движение воды при различных режимах, напорный бак, емкость с раствором красителя, подаваемого открытием краника по трубке во входное сечение стеклянной трубы. Для измерения расхода воды в стеклянной трубе служат мерная емкость и секундомер.

Вода в напорный бак подается по питающему трубопроводу открытием вентиля из резервуара лаборатории. Для поддержания уровня воды в напорном баке во время опытов на постоянной отметке имеется переливное устройство. Температура воды в напорном баке измеряется термометром.

Регулирование расхода воды, а, следовательно, и средней скорости ее движения в стеклянной трубе, осуществляется краном. На стеклянной трубе имеются пьезометры для определения потерь напора по длине \(h_l\) (по разности их показаний).

Схема установки для изучения режимов движения жидкости

Цель работы:

Убедиться на опыте путем окрашивания струйки воды в стеклянной трубе в существовании ламинарного и турбулентного режимов.
Вычислить по данным опытов, проведенных на этой трубе, числа Рейнольдса при ламинарном и турбулентном режимах, сравнить их с критическим, убедиться, что при ламинарном режиме \(Rе < Re_{кр}\) , а при турбулентном – \(Rе > Re_{кр}\).
Построить по опытным данным график \(\lg h_l = f (\lg v)\), определить с его помощью критическую скорость \(v_{кр}\), а через нее вычислить критическое число \(Re_{кр(d)} = \frac{v_{кр} d}{\nu} \).
Подтвердить с помощью графика \(\lg h_l = f (\lg v)\), что при ламинарном режиме потери напора по длине \(h_l\) пропорциональны средней скорости в первой степени, а при турбулентном ‒ в степени \(1,75 ≤ m ≤ 2\).

Порядок выполнения работы и обработка опытных данных

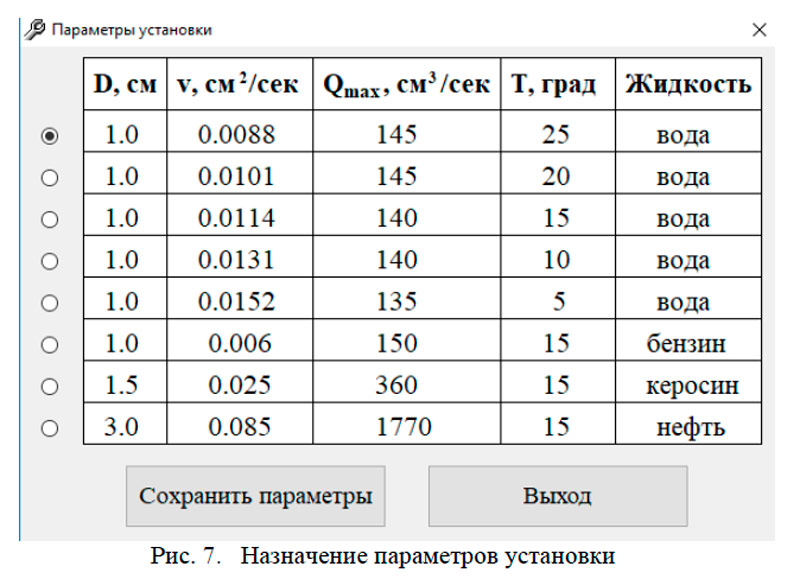
Перед началом работы необходимо в установочном файле выбрать исследуемую жидкость и ее характеристики (см. рис. 7). Выбор производится самостоятельно или по указанию преподавателя.

Далее лабораторная установка запускается в следующем порядке:

Открыть подающий вентиль на питающем трубопроводе и наполнить водой напорный бак настолько, чтобы работало переливное устройство.
Открыть незначительно регулирующий вентиль на стеклянной трубке, чтобы скорость движения воды в ней была небольшой (вода должна течь тонкой струйкой).
Приоткрыть краник на емкости с красителем и направить в стеклянную трубку небольшое количество раствора красителя, чтобы окрашенная струйка воды представляла собой отчетливо выраженную нить по всей длине трубы.
Измерить с помощью мерной емкости и секундомера расход воды \(Q\) в трубе.
Измерить температуру воды в напорном баке термометром.
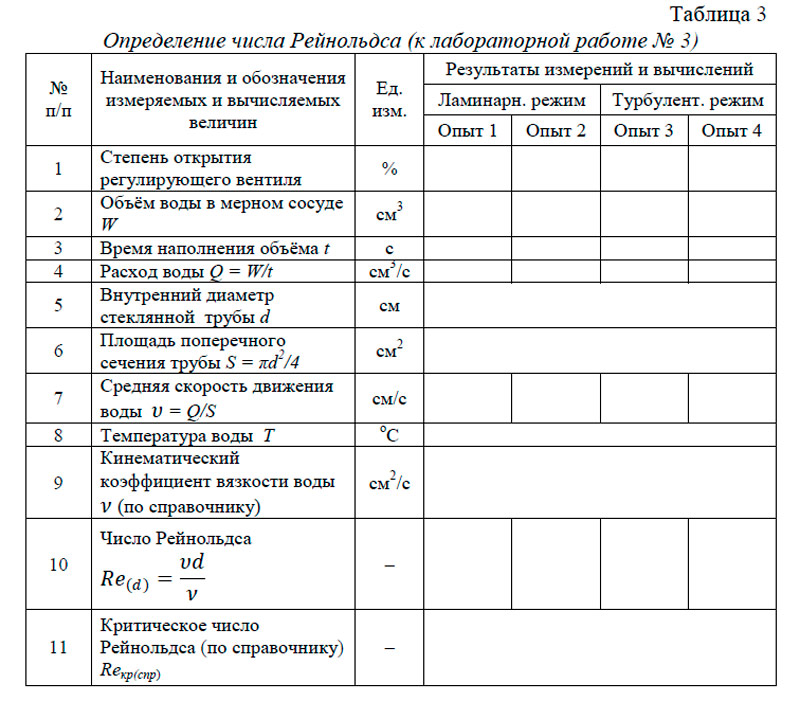
Результаты измерений записать в таблицу 3.
Увеличить открытием регулирующего вентиля скорость движения воды в стеклянной трубе, но так, чтобы окрашенная струйка жидкости сохранялась, т.е. чтобы режим остался ламинарным и, выполнив те же измерения, что и в первом опыте, записать их результаты в табл. 3.
Дальнейшим увеличением открытия регулирующего вентиля создать в стеклянной трубке турбулентный режим (об этом будет свидетельствовать интенсивное перемешивание с водой раствора красителя) и выполнить третий и четвертый опыты так, как описано выше. Результаты измерений записать в табл. 3.
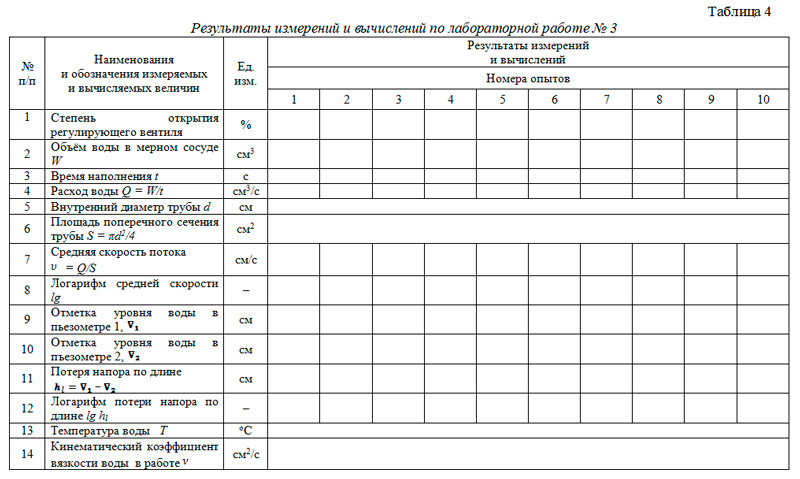
Для заполнения таблицы 4 сделать десять аналогичных опытов, увеличивая в каждом опыте открытие регулирующего вентиля в диапазоне от 0 до 100 % так, чтобы 4‒5 замеров были выполнены в ламинарном режиме, а 5‒6 ‒ в турбулентном. (Замеры показаний пьезометров следует проводить в центре экрана). Результаты измерений записать в табл. 4.
Выполнить все вычисления, предусмотренные табл. 3 и 4.
Построить в масштабе по данным табл. 4 график \(\lg h_l = f (\lg v)\) и определить с его помощью критическую скорость \(v_{кр}\), а через неё и \(Re_{кр(оп)} = \frac{v_{кр} d}{\nu} \), а также показатели степени \(m_л\), \(m_т\) и коэффициенты пропорциональности \(B_л\) и \(B_т\) (см. рис. 5).
Сделать вывод и дать заключение по результатам работы.

Основные контрольные вопросы к лабораторной работе № 3

Назовите режимы движения жидкости и укажите их характерные особенности.
Поясните, что такое критерий Рейнольдса, и назовите факторы, от которых он зависит, и укажите, в чем заключается его физический смысл?
Поясните, что такое критическое число Рейнольдса?
Поясните, каким образом при гидравлических расчётах определяют режим движения жидкости и, с какой целью?
Поясните, что такое критическая скорость, от каких факторов она зависит, и как её определяют?
Напишите и поясните аналитические зависимости потерь напора по длине от средней скорости потока при ламинарном и турбулентном режимах движения жидкости.
Изобразите график зависимости потерь напора по длине от средней скорости (в логарифмических координатах) и дайте пояснения к нему.
Поясните, как определяются \(Re\) и \(Re_{кр}\) для труб некруглого сечения?
Поясните, почему график \(h_l = f(v)\) строят в логарифмических координатах?
Поясните, что такое гидравлический радиус и что он характеризует?