Лабораторная работа № 2: «Определение опытным путем слагаемых уравнения Д.Бернулли»

Автор: Евгений Коноплев

к.т.н., профессор

Автор: Илья Образцов

к.т.н., ведущий инженер ИРТ ТвГТУ

Автор: Александр Яблонев

д.т.н., зав. кафедрой ГТиГП

Лабораторная работа № 2: «Определение опытным путем слагаемых уравнения Д.Бернулли при установившемся неравномерном движении жидкости в напорном трубопроводе».

Вводная часть

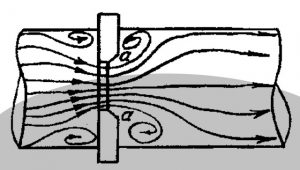
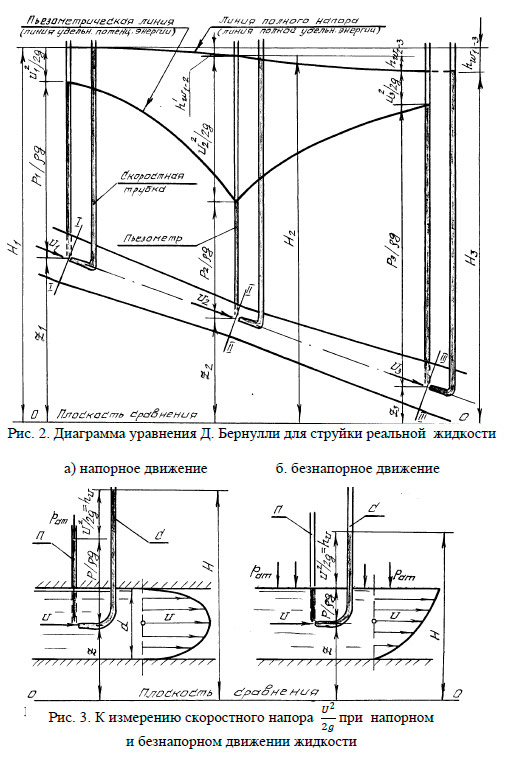
Для двух произвольно выбранных живых сечений \(I‒I\) и \(II‒II\) струйки реальной жидкости при установившемся движении (рис. 2) уравнение Д. Бернулли имеет вид:

\(z_1 + \frac{p_1}{\rho g} + \frac{U_1^2}{2g} = z_2 + \frac{p_2}{\rho g} + \frac{U_2^2}{2g} + h_{W_{1-2}} \), (7)

Слагаемые, входящие в уравнение (7), можно истолковать с геометрической и энергетической точек зрения.

С геометрической точки зрения, слагаемые уравнения (7) являются высотами (напорами):

\(z\) – геометрическая высота (напор), т. е. превышение центра тяжести рассматриваемого поперечного сечения струйки над плоскостью сравнения 0‒0, выбираемой произвольно;

\(\frac{p}{\rho g}\) – пьезометрическая высота, т.е. высота подъема жидкости в пьезометре, подключенном к центру тяжести рассматриваемого сечения струйки, отвечающая гидродинамическому давлению \(p\) в этой точке;

\(\frac{U^2}{2g}\) – скоростная высота (напор), отвечающая местной скорости \(U\), т. е. скорости в центре тяжести сечения;

\(z + \frac{p}{\rho g}\) – гидростатический напор;

\(z + \frac{p}{\rho g} + \frac{U^2}{2g} = H\) – полный напор в рассматриваемом сечении струйки;

\(h_{W_{1-2}} = H_1 — H_2\) – потеря полного напора, т.е. часть полного напора, затраченная на преодоление гидравлических сопротивлений на пути между сечениями \(I‒I\) и \(II‒II\).

С энергетической точки зрения, слагаемые уравнения (7) представляют собой разновидности удельной энергии, а именно:

\(z\) ‒ удельная потенциальная энергия положения жидкости в рассматриваемом сечении струйки;

\(\frac{p}{\rho g}\) ‒ удельная потенциальная энергия давления;

\(z + \frac{p}{\rho g}\) – удельная потенциальная энергия жидкости;

\(\frac{U^2}{2g}\) ‒ удельная кинетическая энергия движения жидкости;

\(z + \frac{p}{\rho g} + \frac{U^2}{2g}\)‒ полная удельная энергия;

\(h_{W_{1-2}}\) ‒ потеря полной удельной энергии струйки, т.е. части ее, затраченной на преодоление работы сил внутреннего трения, обусловленного вязкостью жидкости.

Удельной энергией называется энергия, приходящаяся на единицу веса жидкости.

Величины слагаемых уравнения (7) могут быть определены опытным путем следующим образом:

\(z\) – геометрическим нивелированием или измерением линейкой;

\(\frac{p}{\rho g}\) ‒ с помощью пьезометрической трубки (пьезометра);

\(\frac{U^2}{2g}\) ‒ по разности отметок уровней жидкости в скоростной и пьезометрической трубках, подключенных к рассматриваемой точке живого сечения струйки;

\(h_{W_{1-2}}\) ‒ по разности отметок уровней воды в скоростных трубках, подключенных к сечениям \(I‒I\) и \(II‒II\) струйки реальной жидкости.

Скоростная трубка (трубка Пито) (рис. 3) представляет собой трубку, верхний конец которой открыт в атмосферу, а нижний изогнут навстречу скорости \(U\) в рассматриваемой точке потока жидкости. Благодаря этому, у входа в изогнутый конец скоростной трубки кинетическая энергия частицы жидкости преобразуется в потенциальную энергию давления столба жидкости высотой \(h_U = \frac{U^2}{2g}\).

Поскольку срез нижнего конца скоростной трубки перпендикулярен вектору скорости, а срез нижнего конца пьезометра параллелен, уровень жидкости в скоростной трубке всегда устанавливается выше, чем в пьезометре, на величину \(h_U = \frac{U^2}{2g}\).

Прибор, объединяющий конструктивно пьезометрическую (П) и скоростную (С) трубки, называется трубкой Пито-Прандтля и широко применяется для измерения скорости движения жидкости: \(U = \sqrt{2gh_U}\).

Для двух сечений потока реальной жидкости уравнение Д.Бернулли имеет вид:

\(z_1 + \frac{p_1}{\rho g} + \frac{\alpha_1 v_1^2}{2g} = z_2 + \frac{p_2}{\rho g} + \frac{\alpha_2 v_2^2}{2g} + h_{W_{1-2}} \), (8)

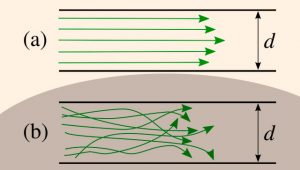
где \(\frac{\alpha v^2}{2g}\) ‒ скоростной напор, отвечающий средней скорости \(v = \frac{Q}{S}\) потока жидкости в рассматриваемом живом сечении (здесь \(Q\) ‒ расход потока жидкости; \(S\) ‒ площадь живого сечения потока); \(h_{W_{1-2}}\) ‒ потеря полного напора (полной удельной энергии) на преодоление работы сил внутреннего и внешнего трения на пути между живыми сечениями потока жидкости \(I‒I\) и \(II‒II\); \(\alpha\) ‒ коэффициент Кориолиса (корректив кинетической энергии), учитывающий неравномерность распределения местных скоростей \(U\) по живому сечению потока, обусловленную вязкостью жидкости.

Величина \(\alpha\) зависит от режима течения жидкости и вида движения. Так, при равномерном движении для ламинарного режима \(\alpha = 2,0\), а для турбулентного ‒ \(\alpha = 1,05…1,15\).

Слагаемые уравнений (7) и (8) в различных живых сечениях можно изображать графически в виде диаграммы уравнения Д. Бернулли, дающей наглядное представление о перераспределении по пути движения жидкости потенциальной и кинетической энергии, а также о характере убывания полной энергии.

Описание установки

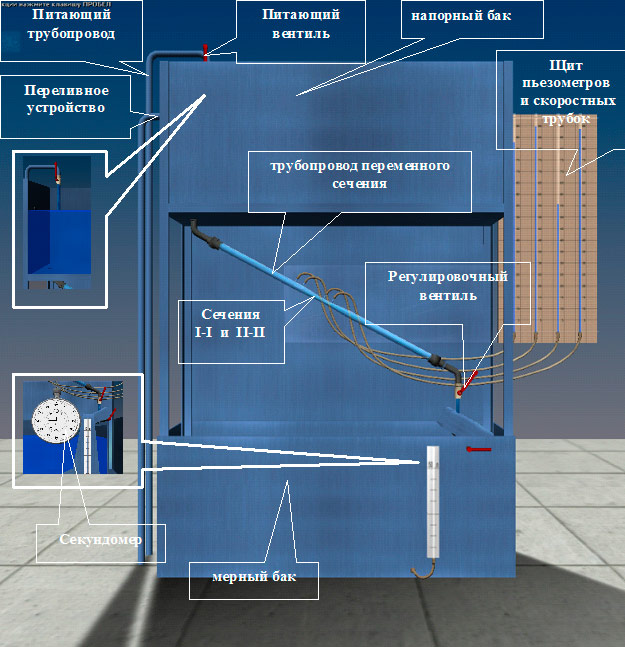
Установка (рис. 4) представляет собой трубопровод переменного сечения с напорным баком, вода в который подается по питающему трубопроводу открытием вентиля. Напорный бак снабжен переливным устройством для поддержания уровня воды на постоянной отметке, чтобы обеспечить в трубопроводе переменного сечения установившееся движение жидкости. К сечениям \(I‒I\) и \(II‒II\) трубопровода переменного сечения подключены пьезометры и скоростные трубки для измерения величин \(z + \frac{p}{\rho g}\) и \(z + \frac{p}{\rho g} + \frac{U^2}{2g}\). Величина расхода воды в трубопроводе переменного сечения регулируется вентилем. Для измерения расхода воды имеются мерный бак и секундомер.

Цель работы.

Определить опытным путем и методом вычислений слагаемые \(z\), \(\frac{p}{\rho g}\), \(\frac{U^2}{2g}\) уравнения Д. Бернулли для сечений \(I‒I\), \(II‒II\), \(III‒III\), а также потери полного напора \(h_{W_{1-3}} \) между сечениями \(I‒I\) и \(III‒III\).
Вычислить средние скорости потока \(v\) и отвечающие им скоростные напоры \(\frac{U^2}{2g}\) для указанных живых сечений потока жидкости.
Построить в масштабе по опытным данным пьезометрическую линию и линию полного напора.

схема установки Д.Бернулли — Фото: Рис. 4. Схема установки для экспериментальной иллюстрации слагаемых уравнения Д.Бернулли

Порядок выполнения работы и обработка опытных данных

При закрытом регулировочном вентиле открыть питающий вентиль для заполнения напорного бака и трубопровода переменного сечения водой. При этом следует обратить внимание на уровни воды в пьезометрических и скоростных трубках. Эти уровни при отсутствии воздуха в системе должны быть на одной отметке.
Открыть регулировочный вентиль до значения, указанного преподавателем. Обратить внимание на то, что трубопровод переменного сечения работает полным сечением, а уровень воды в напорном баке — постоянный.
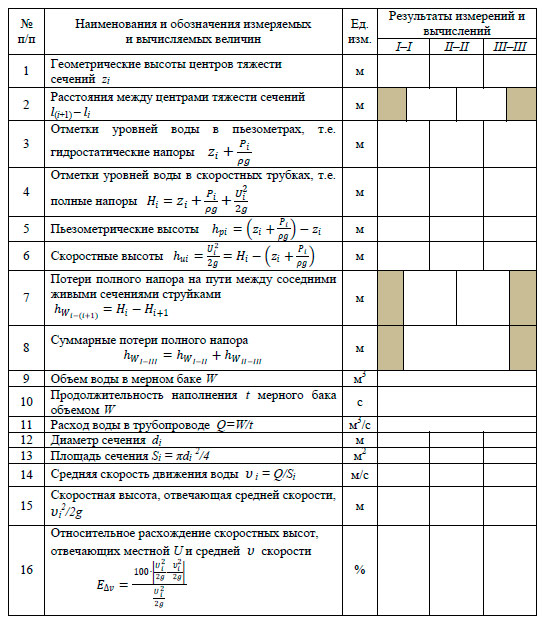
Измерить с помощью мерного бака и секундомера расход воды. Затем измерить геометрические высоты \(z\) центров тяжести сечений \(I‒I\), \(II‒II\) и \(III‒III\) относительно плоскости сравнения 0‒0, отмеченной на установке.
Определить по шкалам отметки уровней воды в пьезометрах и скоростных трубках в сечениях \(I‒I\) и \(II‒II\). Уровень воды в приборах при снятии с них показаний должен устанавливаться в середине экрана. Результаты всех измерений записать в табл. 2.
Выполнить все вычисления, предусмотренные табл. 2. Для сечения \(III‒III\) числовые значения величин (см. строки 6 и 12…16) принять аналогичными сечению \(I‒I\). Потери полного напора \(h_{W_{2-3}} \) (см. строку 7) между сечениями \(II‒II\) и \(III‒III\) принять равными потерям напора \(h_{W_{1-2}} \) между сечениями \(I‒I\) и \(II‒II\). Остальные величины для сечения \(III‒III\) (см. строки 3…5) следует определить с привлечением уравнения Д. Бернулли (см. уравнение 7) и рис. 2, вычерченного в масштабе.
Построить в масштабе по полученным данным линии полного напора и пьезометрическую.
Сделать вывод и дать заключение по результатам работы.

Основные контрольные вопросы к лабораторной работе № 2

Поясните геометрический смысл слагаемых уравнения Д. Бернулли.
Поясните энергетический смысл слагаемых уравнения Д. Бернулли.
Как называется коэффициент \(\alpha\), входящий в уравнение Д. Бернулли для потока реальной жидкости, что он учитывает, от чего зависит его величина и каков его физический смысл?
Объясните, чем обусловлены потери полного напора, и каков их энергетический смысл?
Поясните, что понимают под термином «удельная энергия»?
Объясните термины «местная скорость» и «средняя скорость» и укажите, как определяют эти скорости?
Поясните, что такое скоростная трубка и трубка Пито-Прандтля?
Поясните, что такое линия полного напора и пьезометрическая линия; что будут представлять собой эти линии при равномерном движении реальной жидкости?
Что понимают под термином «живое сечение потока жидкости»?
Охарактеризуйте движение жидкости на пути между сечениями \(I‒I \ldots\) \(II‒II\), исходя из классификации движений жидкости.

Таблица 2

Результаты измерений и вычислений по лабораторной работе № 2 по изучению слагаемых уравнения Д. Бернулли